Graphs Of Secant And Cosecant Functions Worksheet – You’ve found the right place if you are looking for worksheets of graphing functions. There are many types of graphing function to choose from. For example, Conaway Math has Valentine’s Day-themed graphing functions worksheets for you to use. This is a great way to help your child learn about these functions.
Graphing functions
To analyze data and create graphs, graphing functions worksheets can be used. Students will be able to use graphing functions worksheets in order to solve problems and compare data. They will also learn about the different types of graphs. Some worksheets focus on graphing inverse functions and inverse relations. One worksheet may show the graphs for a function while another shows graphs for a function and its inverse.
The first step to graphing a function involves identifying the x-intercept or y-intercept. Next, students will need to complete the input-output tableau. The function will be graphed by them.
How to identify their shape
One of the first steps to graphing functions is to identify their shapes. Functions generally have positive values. If x=2, the graph of f(x) will take positive value, and if x=1, the graph of k(x) will take negative value.
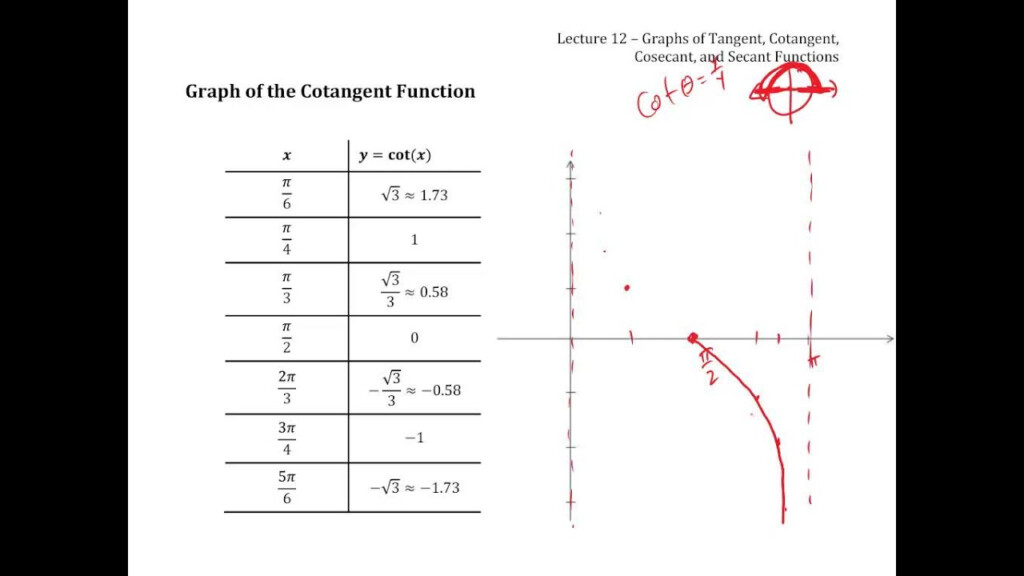
Graphs of different functions have similar shapes, but they can also have different shapes. A graph of a function can be identified by its domain, range and x-intercepts. This graph can be used to calculate the value of the function.
Identifying their property
Graphing functions have two basic properties: a domain and range. A real function has a domain and range of R. For example, y=3x is a real function. One-to-one functions have one output value for every input value.
Continuous functions have no jumps in their graph; instead, the values of continuous functions approach the value x at each point. The opposite is true for functions with open intervals. An open interval is one that stretches from negative to positive. A graphing function may have multiple intervals of its domain.
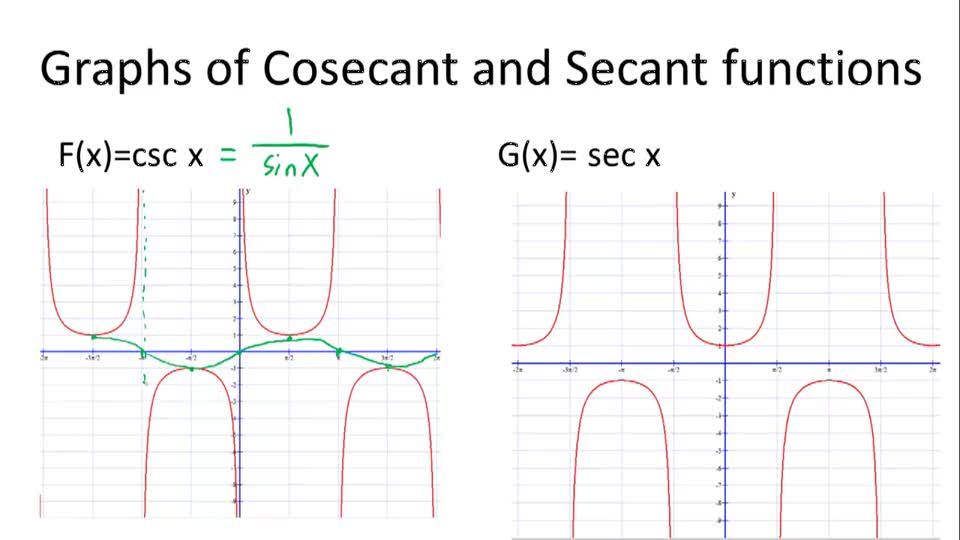
When x is replaced by a negative number, an odd function will have an inverse. Its inverse is f(-x). An example of an odd function is a trigonometric sine function. It is also known as a cosecant function. Graphing a linear function using a computer algebra system is an effective way to explore the properties of a function. The function can then be modelled by creating a computational model.
Identifying their asymptotes
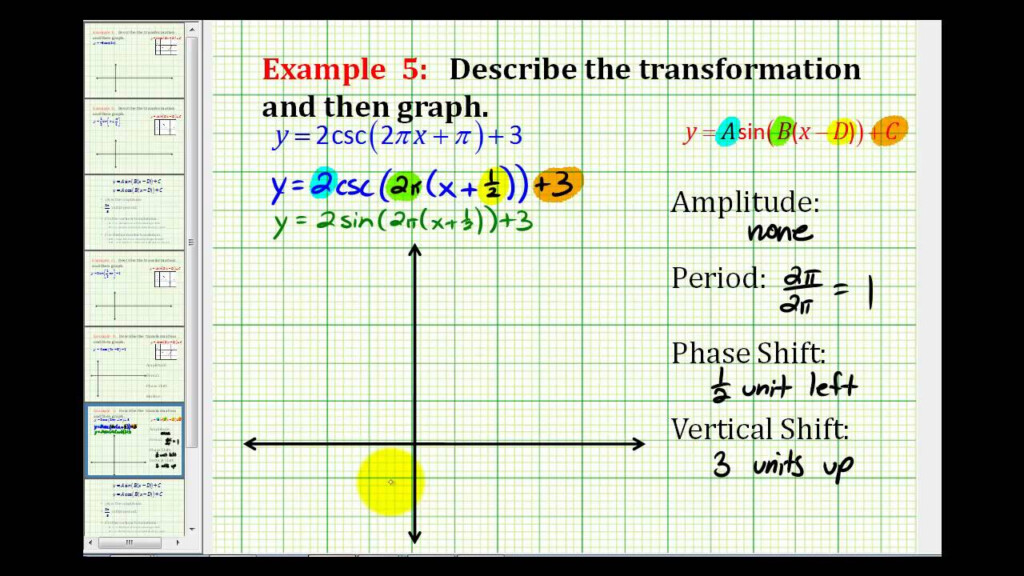
When graphing functions, it is important to identify their asymptotes. The horizontal asymptote is a function whose denominator equals zero. You should search for a vertical asymptote if the denominator does not equal zero. Otherwise, you should avoid this type of asymptote. Horizontal asymptotes can be identified by performing a high-order term analysis.
The point at which a function reaches its maximum value is called the asymptote. This will cause the graph to be either vertical or horizontal. Horizontal asymptotes are marked with vertical dashed lines. If you graph a function that has a zero numerator, it can lead to asymptotes that are so close together that it is hard to tell the difference.
A rational function can be graphed in the same way as a linear function. It will be necessary to compare the denominator’s degree with that of the numerator.
Identify their vertex
Students need to identify their vertex in order to comprehend a graphing function. Students must be able to determine the vertex of a graph by its x and y values. The point at which the x- and y-values meet is called the vertex of a parabola.
Students must identify the vertex when graphing quadratic functions. Then, they must convert the quadratic function’s standard form to its vertex form. They should also be able to locate the zeros in the quadratic functions. These graphing worksheets are useful for students to understand quadratic functions.