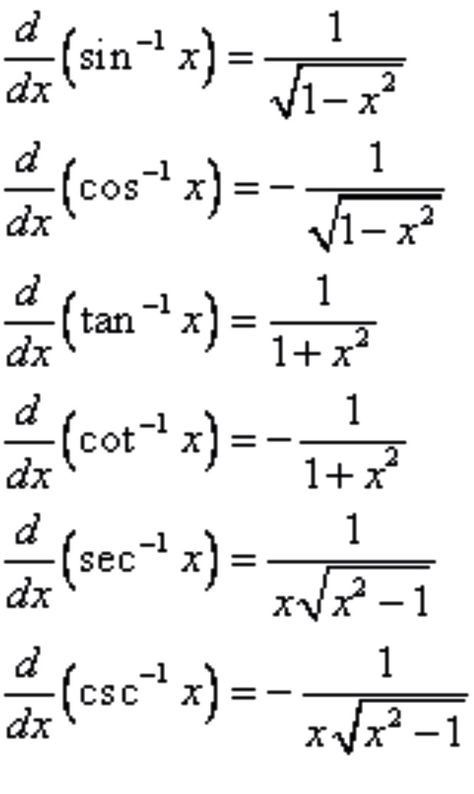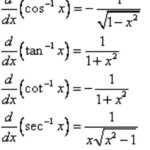Graphing Derivatives Of Functions Worksheet – If you’re looking for graphing functions worksheets, you’ve come to the right place. There are several different types of graphing functions to choose from. Conaway Math offers Valentine’s Day-themed worksheets with graphing functions. This is a great way for your child to learn about these functions.
Graphing functions
To analyze data and create graphs, graphing functions worksheets can be used. Students will be able to use graphing functions worksheets in order to solve problems and compare data. They will also learn about the different types of graphs. Some worksheets focus on graphing inverse functions and inverse relations. For example, one worksheet shows the graphs of a function, while another includes graphs of a function and the inverse of its domain.
The first step to graphing a function involves identifying the x-intercept or y-intercept. Next, students will need to complete the input-output tableau. The function will be graphed by them.
Identifying their shape
Identifying the shapes of different functions is one of the first steps in graphing them. Functions generally have positive values. If x=2, then the graph of function f(x), will take positive value. If x=1, then the graph graph of function k(x), will take negative value.
Graphs of different functions have similar shapes, but they can also have different shapes. A graph of a function can be identified by its domain, range and x-intercepts. This graph can be used to calculate the value of the function.
Identifying their property
Two basic properties of graphing functions are a domain (or range) and a range (or range). Real functions have a domain and a range of R. For instance, y=3x would be a real function. One-to-one functions have one output value for every input value.
A continuous function has no jumps in its graph; instead, its values approach the value of x at every point. Open intervals are the opposite. An open interval is one that extends from negative to positive. An open interval is a graphing function that has multiple domains.
An odd function has an inverse when x is replaced with a negative number. Its inverted form is f(x). A trigonometric sine function is an example of an odd function. It is also known as a cosecant function. It is possible to graph a linear function with a computer algebra system. This allows you to examine the properties of a function. The function can then be modelled by creating a computational model.
Identifying their asymptotes
When graphing functions, you should identify their asymptotes. The horizontal asymptote is a function whose denominator equals zero. You should search for a vertical asymptote if the denominator does not equal zero. You should avoid this type if possible. You can identify horizontal asymptotes by performing a highest order term analysis.
The point at which a function reaches its maximum value is called the asymptote. This will cause the graph to be either vertical or horizontal. Horizontal asymptotes are marked with vertical dashed lines. If you graph a function that has a zero numerator, it can lead to asymptotes that are so close together that it is hard to tell the difference.
Graphing a rational function is similar to graphing a linear function. You will have to compare the degree of the denominator with the degree of the numerator.
Identifying their vertex
Identifying their vertex is important for students to understand a graphing function. Students must be able to determine the vertex of a graph by its x and y values. The point at which the x- and y-values meet is called the vertex of a parabola.
When graphing quadratic functions, students must first identify the vertex of the function. They must then convert the standard form of the quadratic function to its vertex form. They must also know how to find the zeros of the quadratic function. These graphing worksheets are useful for students to understand quadratic functions.